使える統計モデル10選（前編）

統計モデリング（statistical modelling）はデータ解析の方法論の1つです。データ解析の目的は、通常はただの数値や記号の羅列であるデータから、人間が何かしらの判断を行うために有益な情報を引き出すことにあります。データ分析者は、そのままでは意味をなさないデータに対して、折れ線グラフやヒストグラムなどを用いて、人間が判断を行いやすいようにデータの可視化を行います。一方で、時にはニューラルネットワークのような複雑な計算モデルを使ってデータを解析し、まだ観測されていない将来の値を予測させたりします。このように、データから有益な情報を引き出すために、データに対して人為的な視点や事前知識、数学的な仮定などを設計する作業をモデリング（modeling）と呼びます。

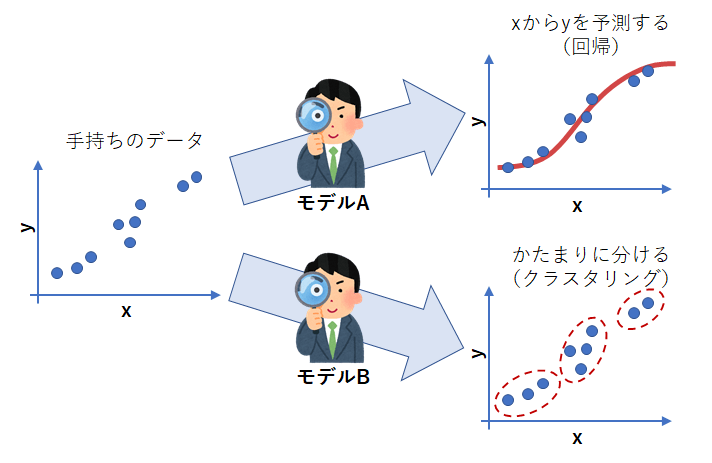
統計モデリングによるデータ解析では、データ自体や解析の目的に合わせて分析者が適切なモデルを設計する必要があります。図１に示すように、モデルとはデータを見通すレンズのようなものです。同じデータに対しても、分析者がどのようなモデルを利用するかによってデータの解釈の仕方や利用の仕方が大きく変わっていきます。絶対的に「正しい」モデルは存在しません。分析者が自身の持つ分析課題に適切だと思うモデルを選択し、その結果得られるものが目的に合致していることが重要です。

統計モデリングの考え方は柔軟性の高いアプローチを提供してくれる一方で、分析者がモデルをゼロから考案し、プログラムで実装まで行うのは多くの場合ハードルが高くなってしまいます。統計モデリングの分野では、すでに世界中の研究者たちが開発した洗練されたモデルが多く存在しているので、分析者は自身が取り組んでいる課題に合うモデルをその中から選び、必要に応じて拡張や単純化などの修正をすれば良いのです。

ここでは、前編と後編に分け、センサーデータ解析、画像認識、自然言語処理など、多岐の分野にわたって実績のあるモデルを適用事例も含めて10個紹介します。本記事ではまず前編として、使用頻度の高い回帰モデルを5つ紹介します。もちろん、統計モデルは無数に存在するため、ここで紹介しているものはほんの一部に過ぎません。あらかじめご理解ください。

統計モデルの入門や最新動向などに関しては下記の記事をご参考ください。
https://www.bigdata-navi.com/aidrops/2423/
https://www.bigdata-navi.com/aidrops/2726/

1 回帰系（教師あり系）
2 まとめ

回帰系（教師あり系）

ここでは、入力データxから出力ラベルyを予測するような回帰モデル（regression model）の代表例を紹介します。

線形回帰モデル

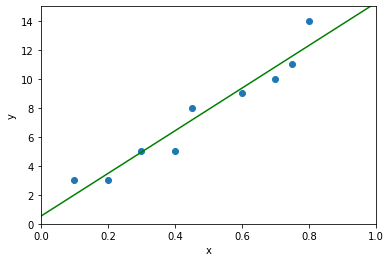
統計学や機械学習を学ぶ際に、もっとも初めに勉強するモデルの１つが線形回帰モデル（linear regression model）です。その名が示す通り、図２に示すような直線の関数によって予測を行います。入力データと出力ラベルが、大まかに比例関係にあれば、このようなシンプルなモデルでも十分に実用的な予測を実現することが可能です。

世の中の多くの現象は線形性で説明することができるため、このモデルは非常に高い汎用性を持っています。「勉強時間が増えればテストの点が上がる」「長い時間スマホを使っているとバッテリーが減る」「土地面積が増加すれば価格が上がる」など、例を挙げればキリがないですが、その多くは線形回帰モデルで大まかではありますが表現することができます。

統計モデル全般的に言えることですが、モデルに対してデータがぴったり当てはまるということはありません。図２に示されるように、モデル（この場合は直線）に対して予測できない誤差が加わったうえでデータ（この場合は各点）が観測されていると仮定します。線形回帰モデルでは、この誤差の傾向には正規分布（normal distribution）が仮定されています。正規分布は対称な分布なので、簡単に言えば、図中で直線に対してデータは上にも下にも同程度の距離で外れることが想定されています。

一般化線形モデル

線形回帰モデルでは、出力ラベルyの誤差に対して正規分布を仮定していました。正規分布以外の確率分布も利用できるように一般化したものが一般化線形モデル（generalized linear model）です。

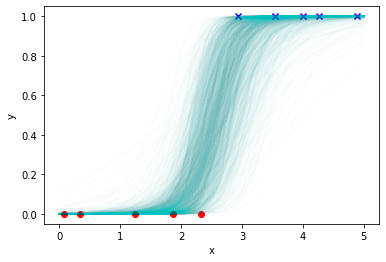
代表的な一般化線形モデルにはロジスティック回帰モデル（logistic regression model）があります。線形回帰モデルでは連続値yを予測することを前提としているため、例えば２値分類（画像を犬か猫か分類するなど）には適していません。ロジスティック回帰モデルでは、観測データyの分布に二項分布（binomial distribution）を仮定することによって、適切な２値の分類を実現します。二項分布はコイン投げの例でよく利用される分布です。図３は、データをロジスティック回帰モデルを用いて分類を行った結果の例です。入力データxに対して、0または1のいずれかの値を取るyの予測を行います。なお、予測の線が束のようにたくさん存在する理由に関しては入門記事をご参考ください。

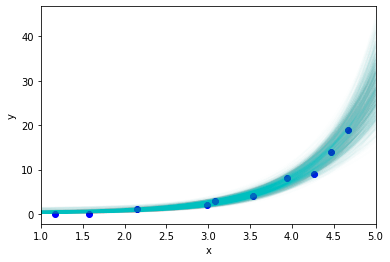
ほかにも便利な一般化線形モデルとして、図４に示すようなポアソン回帰モデル（Poisson regression model）があります。これは、出力ラベルyの分布に対してポアソン分布（Poisson distribution）を利用したものです。ポアソン分布は自然数に対する分布なので、予測対象yが回数（例えば、ある時間内のイベントの発生数など）の場合に使うのが適切でしょう。

階層ベイズモデル

階層ベイズモデル（hierarchical Bayesian model）は、確率分布を使った統計モデリングの利点を生かした手法です。階層ベイズモデルという名前の特定のモデルが存在するわけではなく、一種の既存モデルの拡張法と言えます。

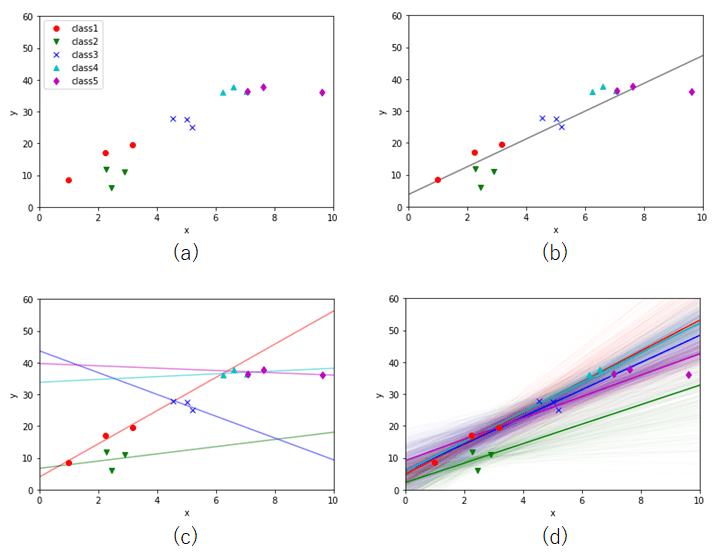
モデルを階層化する目的は、主にデータ全体の傾向と個体（あるいはグループ）の違いを考慮して解析を行いたいからです。例えば図５（a）のようなデータがあったとします。各データ点は5つの異なるクラスが割り当てられています。図５（b）は、クラスの情報を無視し、単純に１つの線形回帰モデルを使って直線のあてはめを行った結果です。予測としては悪くなさそうですが、一部のクラスは予測の直線を大きく外れており、クラスごとの細かい特性はうまく捉えられていないように見えます。図５（ｃ）は逆に、5つのクラスごとに完全に独立な直線を当てはめた場合です。各データ点に対する直線の当てはまり具合は良くなっていますが、予測線が明らかに暴れすぎており、妥当な予測が行えていないように読み取れます。図５（d）は階層ベイズモデルを利用して予測を行った結果です。それぞれのクラスに対しては別々の直線が当てはめられていますが、傾向はそれぞれ似通っているように見えます。この例では、５つすべての直線の位置や向きが共通の傾向（正確には事前分布）を持つような階層化が行われています。共有すべき情報は共有し、なおかつ個別化できる余裕も残しておくことで、（b）や（c）などの単純な線形回帰では実現できないような予測が行えることが階層モデルの強みです。

ガウス過程回帰モデル

ガウス過程回帰モデル（Gaussian process regression model）を利用すれば、一般化線形モデルよりももっと柔軟な回帰モデルを構築することができます。ガウス過程回帰モデルはベイジアンノンパラメトリクス（Bayesian nonparametrics）あるいはノンパラメトリックベイズ（nonparametric Bayes）に代表されるモデルの１つです。

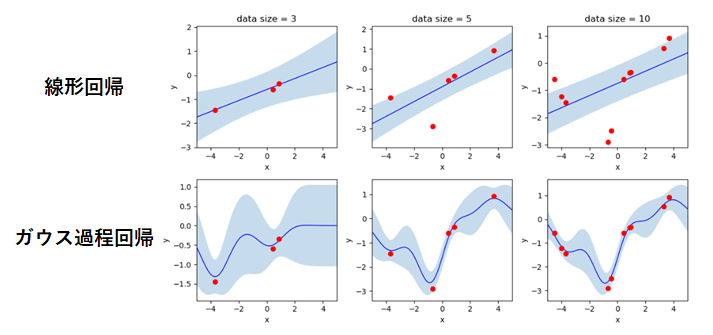
図６はガウス過程回帰モデルと線形回帰モデルによる予測を比較したものです。ノンパラメトリックベイズモデルでは、一般的な統計モデルと異なり、パラメータの個数をあらかじめ固定しません。線形回帰モデルのようなパラメータ数が制限されたモデルでデータを学習させると、データ数が増えるにつれて予測の結果が一定の直線に収束していき、以後データが増え続けても予測はほとんど変化しません。ノンパメトリックベイズモデルであるガウス過程では、データの数に応じて予測が複雑化していくため、このような制約はなく、データの持つより複雑な構造を考慮しながら予測することが可能です。

また、後述するニューラルネットワークモデルと比べて、予測モデルの直観的な設計が行いやすいのがガウス過程の大きな特徴です。例えば、図７にはガウス過程の拡張のバリエーションをいくつか示しています。左から順に、最も単純な指数二次カーネルを使ったもの、データの周期性を検出できる周期カーネルを用いたもの、非線形変換を使って正のyのみに予測域を絞ったものなど、様々な修正・拡張が容易に行えます。

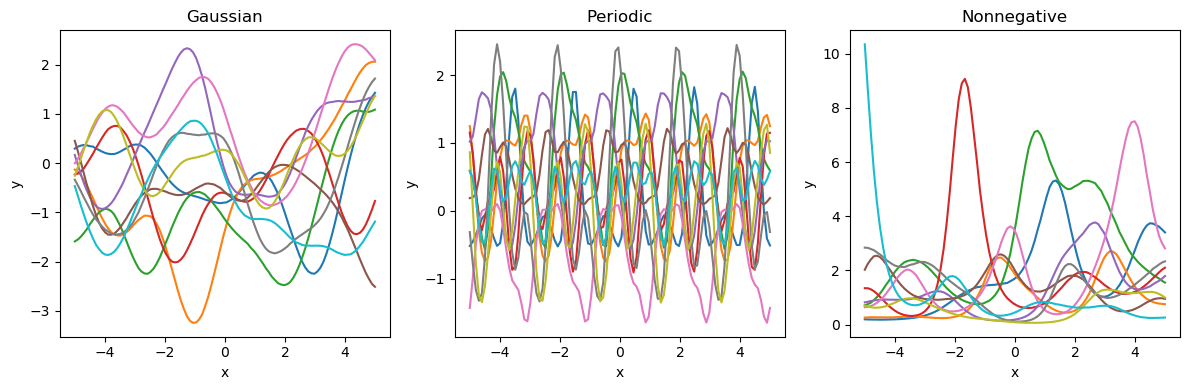
また、従来のガウス過程回帰モデルでは、予測計算に関わる計算量が膨大であるという問題点がありました。しかし、近年では近似的な計算を行うことによって計算量を省くテクニックがたくさん開発されてきています。逆に言えば「計算量さえかければモデルから精緻な予測ができる」という非常に扱いやすいモデルになっています。

ニューラルネットワークモデル

ここ数年で再ブレイクを果たしたのがニューラルネットワークモデル（neural network model）です。元々は脳の神経回路を模したモデルでしたが、現在はそのコンセプトを超え、あらゆる予測課題に利用され始めています。ニューラルネットワークモデルは複数の隠れユニット（hidden unit）に対する非線形変換が何度も重なることによって複雑な関数を表現することができるようになっています。非線形変換は一般化線形モデルで使われるようなシグモイド関数や指数関数をはじめ、ReLUといったものが利用されます。つまり極言すれば、ニューラルネットワークモデルによる回帰は再帰型一般化線形モデルと呼ぶことができるでしょう。

ニューラルネットワークモデルでは、ネットワークの構造に対して様々な工夫を行うことによって、各予測課題に特化したモデルを設計することができます。その中でも最も成功したモデルは、主に画像認識で用いられる畳み込みニューラルネットワークモデル（convolutional neural network model）でしょう。画像データから特徴的な情報を抽出するには畳み込みと呼ばれるフィルタリング処理がよく行われますが、畳み込みニューラルネットワークではこのフィルターをデータから自動的に学習します。

近年の畳み込みニューラルネットワークの構造は非常に巨大なものになっており、与える学習データ数も膨大になっています。例えば2012年に画像認識の精度を大幅に向上させ話題となったモデルは図８のような構成になっています。学習はGPUなどのプロセッサを利用して効率的に行われます。

図８　畳み込みニューラルネットワークの構成例（[Krizhevsky A, Sutskever I, Hinton GE, 2012]から引用）

ニューラルネットワークモデルは汎用性の高いモデル構築の方法論の一つとして考えることができますが、モデルの特性上、パラメータ数が非常に多いため、データに対して簡単に過剰適合（overfitting）してしまうという問題点があります。現在ニューラルネットワークモデルは扱いやすいライブラリが充実しているため利用を始めること自体は容易ですが、モデルが複雑なため、妥当な評価を行うことの方がはるかに難しくなっているのが現状です。ニューラルネットワークを使った予測を行う際には、サービスの本番環境でもしっかり動作するか事前に入念にチェックする必要があります。

まとめ

今回は主に回帰問題に絞ってお勧めのモデルを5つ紹介しました。繰り返しになりますが、単純にxからyを予測するという課題においても、様々なアイデアが存在します。どのモデルが一番優秀か、という議論は全く意味を成しません。個々のモデルの特性を理解し、取り組んでいる問題に対して最も良いと思われるモデルを選択・拡張することが、実務上で統計モデリングを取り扱うための必須スキルになります。

次回記事は生成モデルにフォーカスを移し、それぞれのモデルの設計思想と適用事例を5つ紹介します。

参考文献
須山敦志，杉山将．ベイズ推論による機械学習入門．講談社（2017）
須山敦志．ベイズ深層学習．講談社（2019）
Gelman A, Carlin JB, Stern HS, Dunson DB, Vehtari A, Rubin DB. Bayesian data analysis. CRC press (2013)
Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. InAdvances in neural information processing systems (2012)

須山敦志（すやまあつし）

国内メーカーの研究職，UK のスタートアップの研究職を経て，現在はデータ解析に関するコンサルティングに従事．ブログ「作って遊ぶ機械学習。」にて実践的な機械学習技術に関する情報を発信中．
twitter ID：@sammy_suyama
ブログ：http://machine-learning.hatenablog.com/
著書：ベイズ推論による機械学習入門講談社（2017），ベイズ深層学習講談社（2019）