ベイズ統計・ベイズ機械学習を始めよう
コンピュータやネットワークの技術進化により,これまでにないほどの多種多様なデータを取り扱う環境が整ってきました.中でも統計学や機械学習は,限られたデータから将来を予測することや,データに潜む特徴的なパターンを抽出する技術として注目されています.これらのデータ解析を行うためのツールはオープンソースとして配布されていることが多いため,初学者でも手軽に手を出せるようになってきています.
しかし,データ解析を目的に合わせて適切に使いこなすことは依然としてハードルが高いようです.この原因の一つが,統計学や機械学習が多種多様な設計思想から作られたアルゴリズムの集合体であることが挙げられます.毎年のように国際学会や産業界で新たな手法が考案・開発されており,一人のエンジニアがそれらの新技術を1つ1つキャッチアップしていくのは非常に困難になってきています.
1つの解決策としては,幅広いデータ解析の課題に適用できる汎用的な解析技術を身に着けることです.すなわち,自分が取り組んでいる具体的な課題(装置の異常を検出したい,など)に対してオーダーメイドで手法を設計できるような柔軟性の高い技術です.こうすることによって,課題ごとに適切なアルゴリズムを大量の学術論文やオープンソースのソフトウェアから探してくるといった手間が省くことができ,課題解決自体によりフォーカスすることができます.ベイズ推論(Bayesian inference)に基づく解析手法は,まさにこのような機能を提供する汎用的なフレームワークです.
本記事では,ベイズ手法の観点から見た近年のデータ解析を俯瞰し,初学者の道標となることを目標とします.個々の技術やモデルに関する数理的な解説は省きますので,もっと詳しく知りたい方は最後の参考文献などをご覧ください.
目次
ベイズ統計の基本的な考え方
ベイズ統計は「確率モデルの設計」と「推論計算」の2ステップから成り立っています.
確率モデル(probability model)または統計モデル(statistical model)とは,今解析しているデータに対して与える数理的な仮定(データ生成過程やデータの持つ性質など)を,確率分布(probability distribution)などの道具を使って表現した設計図のようなものです.代表的な確率分布には,0~1の一様な実数を生成する一様分布(uniform distribution)や,サイコロの試行でお馴染みの多項分布(multinomial distribution),釣り鐘型の正規分布(normal distribution)あるいはガウス分布(Gaussian distribution)といったものがあります.これらの基本的な部品を適切に組み合わせることによって,課題に沿った確率モデルを構築します.
ベイズ統計の分野では,すでに先人たちが開発した多くの便利な確率モデルがあります.それらの中には汎用的な時系列データの予測に使えるものから,自然言語処理に特化したようなモデルまで幅広くあります.
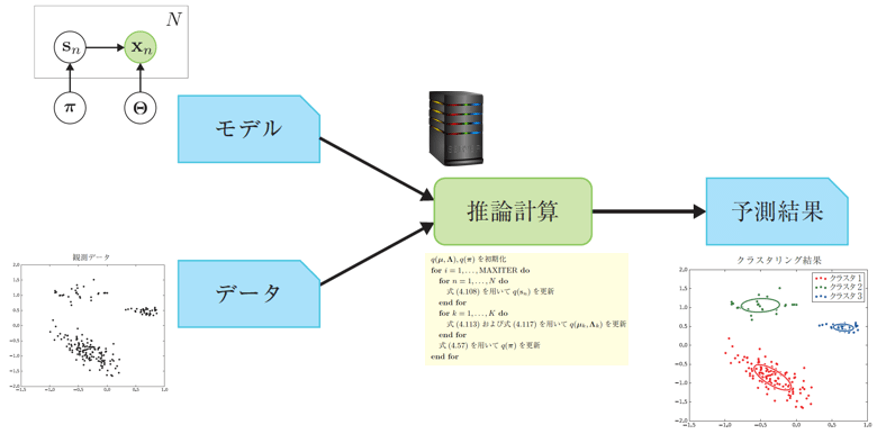
さて,モデルは単体ではただの数式で表された設計図です.モデルに具体的なデータを与え,さらに確率推論(probabilistic inference)を行うことによって何かしらの有用な解析結果を出します.例えば図1では,平面上の複数の点で表現されるデータに対して,ガウス混合モデル(Gaussian mixture model)と呼ばれるモデルを仮定し,推論計算によって結果を可視化したものです.これはデータに潜むまとまりを見つけるための手法で,クラスタリング(clustering)として知られています.
代表的なモデル
ベイズ統計で使用される代表的なモデルとその用途に関して説明します. 大まかに分類すると,モデルは回帰・分類モデルと生成モデルに分けることができます(脚注1:ただし,厳密に両者を分類する必要はありません.なぜなら,両者のアイデアを統合したような発展的なモデルも数多く存在するためです.).
回帰・分類モデル
回帰モデル(regression model)および分類モデル(classification model)は,最も基本的な予測手法です.これらの手法は教師あり学習(supervised learning)とも呼ばれます.入力データxと出力データyを数多く用意し,その間の関数をモデル化するものです.
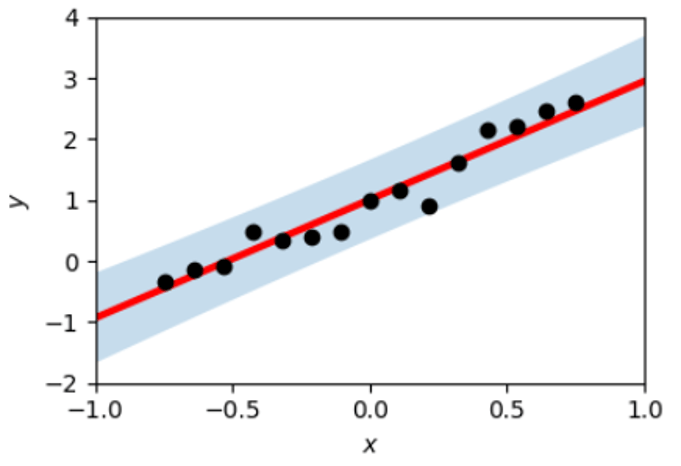
回帰は主に連続値の予測に使われます.最も基本的な回帰モデルは線形回帰モデル(linear regression model)で,図2のように,単純に直線を使ってxとyの関係性をモデル化します.
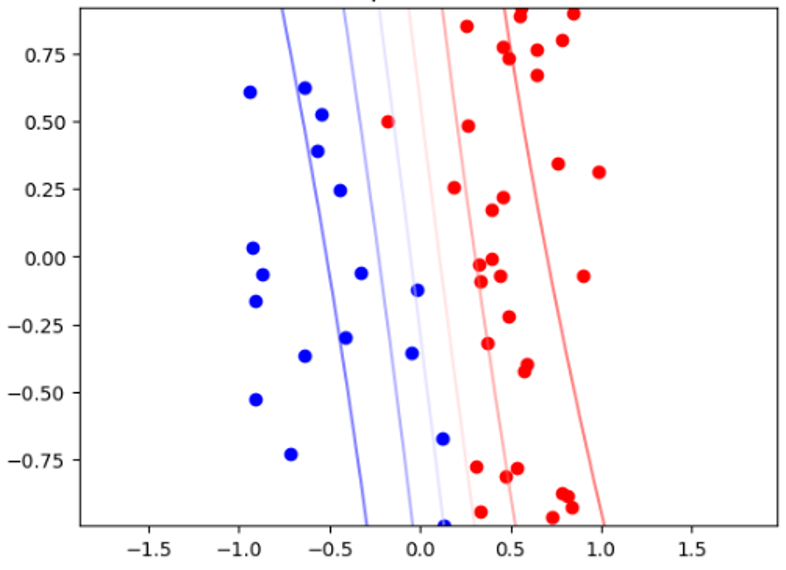
分類は主にデータをいくつかの有限個のカテゴリに判別するために使われます.中でもロジスティック回帰モデル(logistic regression model)は,データ分類に使われる代表的なモデルです(脚注2:回帰と名前がついていますが,分類に使われる場合が多いモデルです.).図3の例では,ロジスティック回帰を使ってデータを2分類したケースを示しています.また,ロジスティック回帰は一般化線形モデル(generalized linear model)の一例としても知られています.
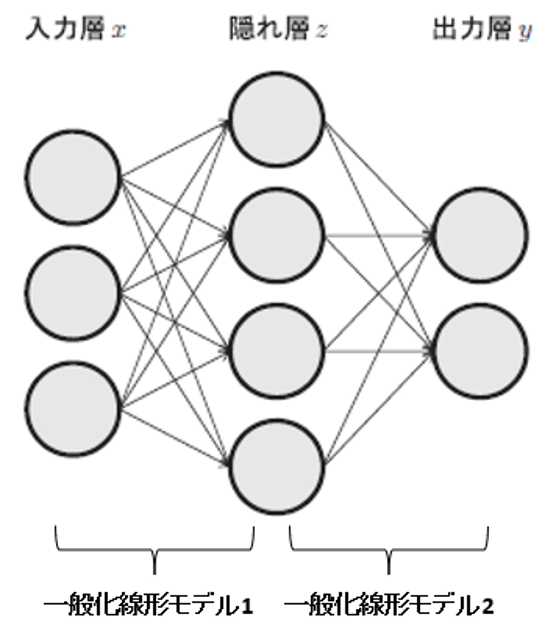
もっと複雑なモデルとしてはニューラルネットワークモデル(neural network model)があります(図4).これは,(ロジスティック回帰のような)一般化線形モデルの出力を,またさらに別の一般化線形モデルの入力に入れるようなモデルです.このような階層化は複数回行うことができ,特に何層にもわたったものを深層学習モデル(deep learning model)と呼びます.
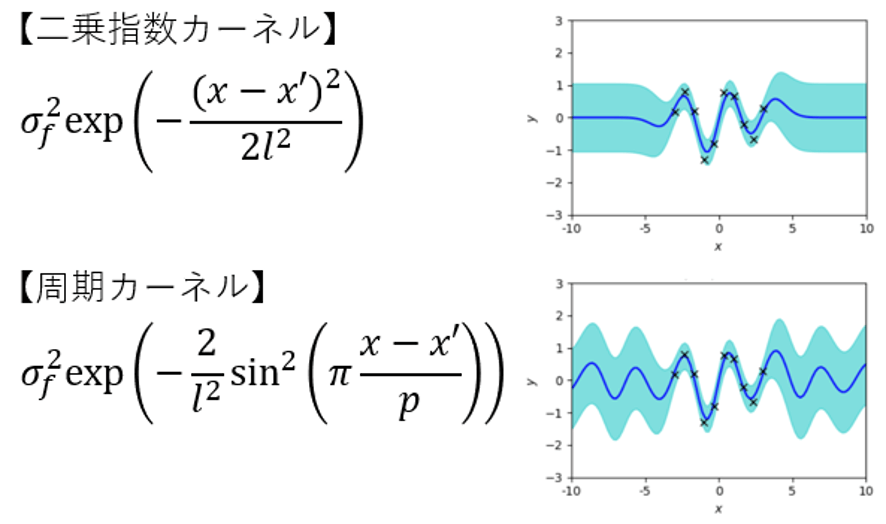
ベイジアンノンパラメトリックモデル(Bayesian nonparametric model)を使えば,より柔軟な回帰モデルを設計することができます.中でもガウス過程回帰モデル(Gaussian process regression model)は,カーネル法(kernel method)と呼ばれる手法に基づいており,カーネル関数(kernel function)を設計することによって,一般化線形モデルよりもはるかに自由度の高い回帰モデルを設計することが可能になります(図5).
生成モデル
生成モデル(generative model)は回帰・分類モデルのようにxとyの関係性を求めるのではなく,データ自体の生成過程を設計する手法です.潜在変数モデル(latent variable model)とも呼ばれます.そのような特性から,主に教師なし学習(unsupervised learning)として利用される機会が多い手法です.
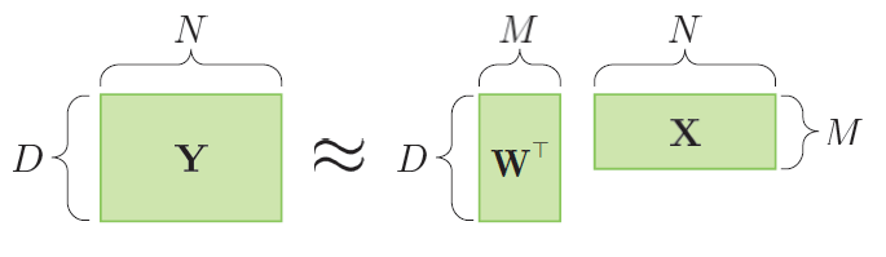
代表的な手法が行列分解モデル(matrix factorization model)です.行列分解モデルでは,図6のYのような行列(matrix)で表されるデータを,よりサイズの小さな2つの行列に分解します.データをよりコンパクトな行列の積で表すことによって,データの潜在的な構造を抽出します.主成分分析(principal component analysis)や因子分析(factor analysis),非負値行列分解(nonnegative matrix factorization)といった手法もこれらに分類されます.また,行列を3次元以上のテンソル(tensor)に拡張したテンソル分解モデル(tensor factorization model)もあります.これらの行列分解モデルは,データの非可逆圧縮や,ECサイトの商品推薦アルゴリズムなどに用いられます.
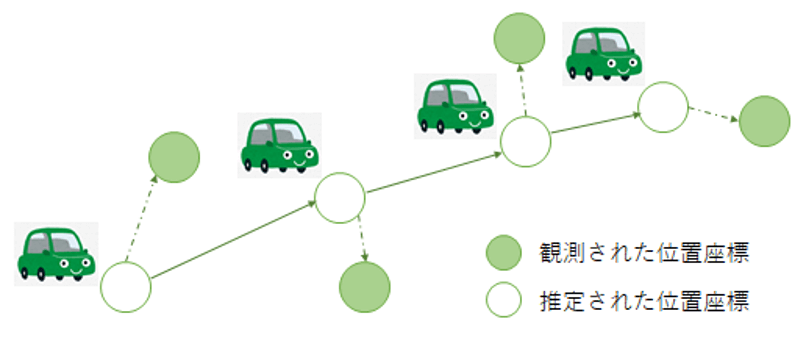
状態空間モデル(state space model)は,主に時系列データの解析に用いられるモデルです.図7のように,観測データの背後に,観測されない潜在的な時間変化が存在していると仮定します.潜在的な変化が離散であるか連続であるかによって,隠れマルコフモデル(hidden Markov model)と線形動的システム(linear dynamical system)に分類されます.隠れマルコフモデルはDNA解析や音声認識,自然言語処理,ジェスチャー認識などの多くの分野に利用されています.線形動的システムはカルマンフィルター(Kalman filter)としても知られており,GPSを用いた移動物体のトラッキングや,商品の需要予測などに使われています.
もっと凝ったモデルとしては,ニューラルネットワークを潜在変数モデルにした変分自己符号化器(variational auto-encoder)や,ガウス過程を教師なし学習に拡張したガウス過程潜在変数モデル(Gaussian process latent variable model)などがあり,様々なデータに対して内在する複雑な構造を抽出することに成功しています.
代表的な推論計算
推論計算は簡単なモデルであれば手計算で出すこともできますが,近年ではベイズ統計のモデルは複雑さを増してきているため,一般的にはコンピュータを使った計算を必要とします.このような計算を行うアルゴリズムは大きく分けて厳密推論(exact inference)と近似推論(approximate inference)があります(脚注3:なお,機械学習の分野では新しいデータに対して予測を実施することを「推論」と呼ぶ場合がありますが,ベイズ統計では推論はより広い意味を持ち,確率的な計算すべてを指します.).
厳密推論
厳密推論が行える例として,線形回帰モデルを考えてみましょう.線形回帰モデルにおける推論計算の目標は,複数与えられた入力データxと出力データyを学習データとし,新しい入力x*に対する予測結果y*を見積もることです.線形回帰モデルのような単純なモデルの場合は,この予測は手計算で厳密に求めることができます.
多数の変数を持つようなより大規模なモデルに対しても厳密推論が計算できる場合があります.特に,モデル内の複数の変数が木構造の関係性を持ち,かつ変数が正規分布などの簡単な分布に従っている場合では,信念伝播法(belief propagation)と呼ばれる効率的な厳密推論アルゴリズムが利用できます.さらに,より一般的な構造を持つモデルに対する厳密推論手法としてはジャンクションツリーアルゴリズム(junction tree algorithm)があります.
近似推論
厳密推論が実行できるのが理想的ですが,実用的なモデルのほとんどは厳密計算を行うにはコンピュータを使っても計算時間がかかりすぎてしまいます.近似推論を使えば,計算の精度は厳密推論と比べて落ちてしまいますが,実用に耐えうる結果を高速に得ることができます.
最もよく使われている近似推論手法はマルコフ連鎖モンテカルロ法(Markov chain Monte Carlo method)と呼ばれている手法群です.代表的なものにはメトロポリス・ヘイスティングス法(Metropolis-Hastings method),ハミルトニアンモンテカルロ法(Hamiltonian Monte Carlo method),ギブスサンプリング(Gibbs sampling)などがあります.
変分推論法(variational inference method)あるいは変分ベイズ法(variational Bayes method)は,一般にマルコフ連鎖モンテカルロ法よりも高速な手法として知られ,近年では利用される機会が増えてきています.特に,先ほど紹介した潜在変数モデルや,ニューラルネットワークモデルといった,複雑なモデルに対して効率良く推論計算を実施することができます.
機械学習や深層学習との関係
ベイズ統計と関連の深い分野に関して簡単に解説します.
機械学習
人間が通常行っているような「学習」の部分をコンピュータで実現しようとするのが機械学習(machine learning)と呼ばれる分野です. 人間の思考能力をコンピュータ上に実現する人工知能(artificial intelligence)の分野から派生した手法ですが,近年の理論的な研究成果から,統計学と区別する意味は薄くなってきています.
ベイズ統計との関りは歴史的に見ても非常に深く,ベイズ統計の考え方から作られた機械学習アルゴリズムも多く存在するほか,既存の機械学習アルゴリズムをベイズ統計の考え方によって再構築するような例も見られます.特に,機械学習の分野でよく利用される方法として,正則化(regularization)と呼ばれる予測を安定化させるための手法や,クラスタリングに使われるk平均法(k-means method)といった教師なし学習の手法がありますが,これらは確率モデルによる解釈を与えることが可能です.
深層学習
深層学習(deep learning)は機械学習の中の1つの手法群であり,大規模なニューラルネットワークモデルを構築することによって画像解析などを行います.
深層学習とベイズ統計の関りも非常に古くから知られています.特に,変分推論法やハミルトニアンモンテカルロ法といった近似推論手法は1990年前後から頻繁に使われるようになり,当時の適用先はニューラルネットワークモデルが主流でした.
また,近年深層学習の性能向上に貢献している多くのテクニックが,ベイズ統計における近似推論手法として解釈されていることが知られています.例えば,ドロップアウト(dropout)やバッチ正規化(batch normalization)と呼ばれるニューラルネットワークの学習テクニックは,1種の変分推論法と見做すことが可能です.また,ニューラルネットワークの隠れ層(hidden layer)に無限の幅を持たせると,ガウス過程モデルと見なせることが知られています.
ツールや書籍など
近年ではベイズ統計を実施するための便利なツールが手軽に手に入るようになってきています.ベイズ統計を駆使して実践的なデータ解析を実施していくには,それらのツールを実務で使っていきながら,並行して書籍などを参照してテクニックや事例を学んでいくのが良いでしょう,
ツール
下記のツールは確率的プログラミング言語(probabilistic programming language)と呼ばれるライブラリです.文字通り確率モデルをプログラミングコードのように記述して設計することができるのが特徴です.推論計算に関しては,ツールが自動的にモデルを解析し,コンパイルおよび実行をしてくれます.
Stan
– 最も広く利用されているベイズ統計ツールです.RやPython,Matlab,Juliaなど様々なプログラミング言語から利用することが可能です.
– https://mc-stan.org/
PyMC
– Python用に設計されたベイズ統計ツールです.MC=Monte Carloと書いてありますが,マルコフ連鎖モンテカルロ法だけではなく変分推論法もサポートされています.現在はPyMC3が主流ですが,PyMC4も開発中です.
– https://docs.pymc.io/
TensorFlow Probability
– Googleが開発した機械学習プラットフォームのTensorFlow上で動作するモデリングツールです.GPUやTPUといったハードウェアを利用した高速化が見込めます.
Pyro
– こちらもPython用です.主に深層学習の確率モデルを構築するためのツールです.
– https://pyro.ai/
以上のように,ベイズ手法はPythonやRを使って実装されることが多いことがわかるかと思います.一方で,アルゴリズムの数理的な理解や,細かいカスタマイズを行って高速なアルゴリズムを構築することを目的とした場合は,科学計算用の言語であるJuliaがお勧めです.
– https://julialang.org/
書籍
ベイズ統計の考え方を理解するためには,ただ単にツールに頼るのではなく,実際に自分で手計算を行うなどして経験を積む必要が出てきます. したがって,理工系の大学1年生レベルの線形代数学と微積分に関しては,基本事項だけでも学んでおくことをお勧めします.
下記の文献は日本語で書かれたお勧めの書籍です.★がついている書籍に関しては,本記事の執筆にあたっても参考にしています.
ベイズ統計やベイズ機械学習に関する入門レベルの書籍としては次のようなものがあります.
– しくみがわかるベイズ統計と機械学習
– ベイズ推論による機械学習入門★
Stanなどのツールを応用した実践書は次のようなものがあります.
– Pythonで体験するベイズ推論
– Pythonによるベイズ統計モデリング: PyMCでのデータ分析実践ガイド
– StanとRでベイズ統計モデリング
– 実践Data Scienceシリーズ RとStanではじめる ベイズ統計モデリングによるデータ分析入門
– Pythonによるデータ分析入門
– Pythonで体験するベイズ推論
理論や発展的な技術に関しては次のような書籍があります.
– トピックモデルによる統計的潜在意味解析
– ガウス過程と機械学習
– ノンパラメトリックベイズ
– ベイズ統計の理論と方法
– パターン認識と機械学習★
– ベイズ深層学習★
国内メーカーの研究職,UK のスタートアップの研究職を経て,現在はデータ解析に関するコンサルティングに従事.ブログ「作って遊ぶ機械学習。」にて実践的な機械学習技術に関する情報を発信中.
twitter ID:@sammy_suyama
ブログ:http://machine-learning.hatenablog.com/
著書:ベイズ推論による機械学習入門 講談社(2017),ベイズ深層学習 講談社(2019)

 フリーランス求人を探す
フリーランス求人を探す






