HomeプログラミングPythonで作って学ぶ統計モデリング

プログラミング

Pythonで作って学ぶ統計モデリング

Pythonで作って学ぶ統計モデリング

近年、AIや機械学習、深層学習といった用語に代表されるように、多種多様のデータを高度なアルゴリズムと計算機の力で解析し、将来予測などの価値を生み出す技術に注目が集まっています。

これらの技術の土台となっているのが、本記事で解説する統計モデリング（statistical modeling） と呼ばれる考え方です。元々は手計算が可能なレベルの比較的シンプルな数学的仮定を置いてデータを解析する方法論として発展しましたが、近年の計算機の性能発達に伴い、従来では取り扱えなかったより複雑なモデルを利用した高度な解析を実施する事例が増えてきています。特に、現在実践で広く使われている機械学習のモデルや、複雑な非線形関数を組み合わせた深層学習モデルなども、その多くは突き詰めれば統計モデルの一種であることが言えます。したがって、統計モデリングはそれ自体がデータ解析に対して有用なアプローチであるだけではなく、様々なAI技術を統一的に理解するためにも必須の概念となっています。

ここでは統計モデリングの基本的な考え方を説明します。また、近年急速に利用が拡大している確率的プログラミング言語（probabilistic programing language）と呼ばれる統計モデリングのためのツールを紹介します。本記事では中でもPythonで気軽に利用ができるPyMC3というツールを使って、シンプルな線形回帰モデルを構築し、その動作を解説します。したがって、Pythonの基本的なプログラミング知識をお持ちであることを前提とします。なお、下記の記事では統計モデリングの最新の技術動向を俯瞰していますので、こちらも併せてご参考ください。

参考：ベイズ統計・ベイズ機械学習を始めよう


BIG DATA NAVI

フリーランス・副業をはじめるなら！

BIGDATA NAVI
AI・データ分析案件で業界最大級のフリーランスエージェント。
非公開案件やエンド直案件など、案件情報多数。
フリサポ
フリーランスへの独立や副業からのスタートをサポート！
カウンセリングや案件情報提供も完全無料で利用できます。
AIジョブキャンプ
機械学習のオンライン講座を無料提供！
独立へのスキルアップサポートで稼げるフリーランスへ！

統計モデリングとは何か

計算機に保存されているデータは、そのままでは単なる数字の羅列に過ぎません。データから意味のある情報を抽出するためには、データに対して何らかの前提・仮定を設定することが必要になってきます。統計モデリングでは特に、「データが生成される過程や、データに成立する性質に関して仮説を置く」ことによってアプローチをします。

入力値xから出力値yを予測する回帰（regression）と呼ばれる課題について例を考えてみましょう。この場合、「仮定」はxとyの関係性に置かれます。これには、単純な直線関係y=ax+bや、周期関数y=sin(ax+b)、指数関数y=exp(ax+b)を使ったものまでさまざまなものが考えられます。このように、データに与える仮定を数理的に記述したものをモデル（model）と呼びます。単一のモデルをあらかじめ仮定したり、複数のモデルをうまく組み合わせるなどして、時系列データの精度の高い予測から画像データの識別といった発展的な課題も同様にして扱えるようになります。

数学的な仮定、すなわちモデルを設計した後は、実際に観測されたデータを突き合わせることによって、観測されていないデータ（例えば株価の将来の値や、センサーデータの欠測値など）に対する統計的な予測を行うことができます。例えば、fig.1は4個の観測データ（入力ｘと出力yの組）に対して、一次関数を使って回帰予測を行った結果です。ひとたび一次関数（具体的には傾きと切片）を求めることができれば、新しい入力ｘが入ってきたときに、その対応する予測値yを計算することができます。この例では、予測に一次関数を指定することは分析者があらかじめ決めます。データに適合するような傾きと切片の計算は、簡単なケースでは分析者が手計算で行うことができます。しかし、モデルが複雑になってくるとこの計算が煩雑になったり、あるいは厳密に計算することが不可能になってくるという問題点があります。

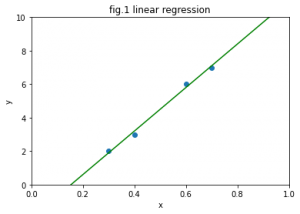
以上をまとめると、統計モデリングのアプローチは次のようなステップになります。

【ステップ１：モデリング】
  • データに対してモデル（数学的な仮定）を設計する。
  • これは分析者自身が行う。
【ステップ２：予測の計算】
  • モデルに対して実際のデータを突き合わせ、予測を行う。
  • これは分析者が行うこともあるが、多くの場合計算が煩雑なため困難。

確率的プログラミング言語とは何か

確率的プログラミング言語は、上記のステップを簡略化してくれる便利なツールです。 ステップ１では、分析者が直感的にモデルを設計しやすいように、プログラムコードとしてモデルを記述できるようになっています。

より重要なのはステップ2です。特に、確率的プログラミング言語は与えられたモデルとデータから自動的に予測結果を出力することが可能になっています。これは分析者が自力で計算結果を導出したり、効率的な計算アルゴリズムを組むことが困難な場合に有効です。

現在、確率プログラミング言語は様々なものが開発されています。 最も利用実績が多いのはStanです。
https://mc-stan.org/

RやPython、Matlab、Juliaなど様々なプログラミング言語から利用することが可能です。また、深層学習モデルの効率的な設計・計算を行うためのツールとしてTensorFlowがありますが、最近ではその計算効率を利用したモデリングツールとしてTensorFlow Probabilityも話題になってきています。
https://www.tensorflow.org/probability

近年では機械学習モデルや深層学習モデルの構築でPythonがデファクトスタンダードとなっていますが、PyMCは文字通りPythonをベースとした確率的プログラミング言語です。本記事ではPyMC3を使って解説を行っていきます。

PyMC3の利用

PyMC3はその名が示す通り、Pythonで記述するためのMCMC（Markov chain Monte Carlo、マルコフ連鎖モンテカルロ）ライブラリです。MCMCに関して詳しい説明は省きますが、これは上記のステップ2の予測計算を行うための計算アルゴリズムであると考えれば良いでしょう。PyMC3以外でも多くの確率的プログラミング言語が同様のアルゴリズムを採用しています。

本記事で解説する例は、Python3.6.9がインストールされている環境を想定しています。下記のサイトを参考に、PyMC3（ver3.7）をインストールします。
https://docs.pymc.io/

また、手っ取り早くPyMC3を体験したい方は、Googleが提供するクラウド上のNotebook環境のColaboratoryが便利です。この記事のプログラムもColaboratoryで実装されています。Googleアカウントを取得していればColaboratoryは無料で利用することが可能です。 https://colab.research.google.com/

PyMC3による線形回帰

ここでは早速、PyMC3を利用した線形回帰モデルによる予測を実践してみましょう。 まず、必要なライブラリをインポートします。

# ライブラリのインポート

import pymc3 as pm
import matplotlib.pyplot as plt
import numpy as np

matplotlibは、データや解析結果をグラフにするためのライブラリです。 numpyは、Pythonでデファクトスタンダードとなっている数値計算用のライブラリです。

次に、今回利用するデータを可視化します。今回は、入力データxから出力データyを予測するような回帰モデルを構築することが目標です。

# データの読み込みと可視化

# データ
X = [0.3,0.4,0.6,0.7]
Y = [2,3,6,7]

# 散布図で可視化
plt.scatter(X, Y)
plt.xlabel('x')
plt.ylabel('y')
plt.xlim([0,1])
plt.ylim([0,10])

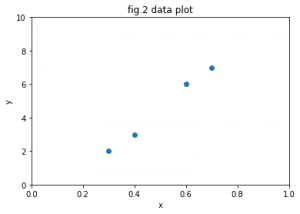
ここでもなるべく話を単純化するために、データの総数は４個のみにしています。fig.2のグラフを見ればわかるように、データはy=ax+bで表すことのできる一次関数で大まかに表現できそうに見えます。一次関数y=ax+bのように、入力データxの線形和で出力データyが表現できるようなモデルを線形回帰モデルと呼びます。

次に、モデリングを行っていきましょう。PyMC3では、正規分布（normal distribution）を利用した線形回帰モデルは次のように書きます。

# 線形回帰モデル

with pm.Model() as model_linear:
  pm_a = pm.Normal('pm_a', mu=0.0, sd=10.0)
  pm_b = pm.Normal('pm_b', mu=0.0, sd=10.0)
  pm_Y = pm.Normal('pm_Y', mu=pm_a * X + pm_b, sd=1.0, observed=Y)

PyMC3では、モデルはwith構文を使って記述します。 ここで記述されるモデルは、「一次関数が、どのような確率的な仮定のもとで実現されているのか」を表しています。 pm_aとpm_bは、それぞれ正規分布に従うと仮定した直線の傾きと切片を表します。 pm_Yの行では、個々の観測データyに仮定されている分布を表しています。つまり、「データはax + bで大まかに表されるが、それにさらに標準偏差が1.0であるような正規分布のノイズが加わって実際のyが観測される」と仮定されていることになります。

さて、PyMC3では、今まさに記述したモデルが具体的にどのような一次関数を仮定しているかを視覚化して確認することができます。ここでは、次のsample_prior_predictive()関数を用いてmodel_linearから100個の一次関数をサンプルしています。

# 一次関数のサンプル

with model_linear:
   prior_samples = pm.sample_prior_predictive(100)

prior_samplesには100個の傾きおよび切片が格納されています。次のように、100個すべての一次関数を可視化してみます。

# 一次関数の可視化

X_range = np.linspace(0,1, 1000)
for i in range(100):
    plt.plot(X_range, [prior_samples['pm_a'][i]*x + prior_samples['pm_b'][i] for x in X_range], 'g-', alpha=0.1)
plt.xlabel('x')
plt.ylabel('y')

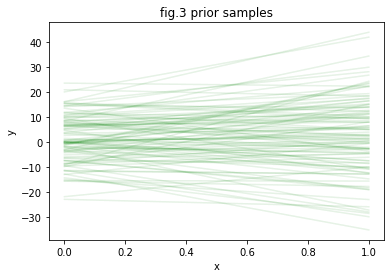
fig.3は実際にサンプルした関数の集合です。さまざまな傾きや切片を持った一次関数が重ね描きされています。この傾向は、pm_aやpm_bに設定された事前分布（prior distribution）のパラメータによって傾向が変わります。すなわちのmuやsdの値を変えることによって、様々な特性を持った一次関数を仮定することができます。これらの値は解析対象の性質に合わせて設定します。このような事前知識の積極的な導入は、特にデータ数が少ない際でも高精度に予測をしたい場合などに極めて有効です。

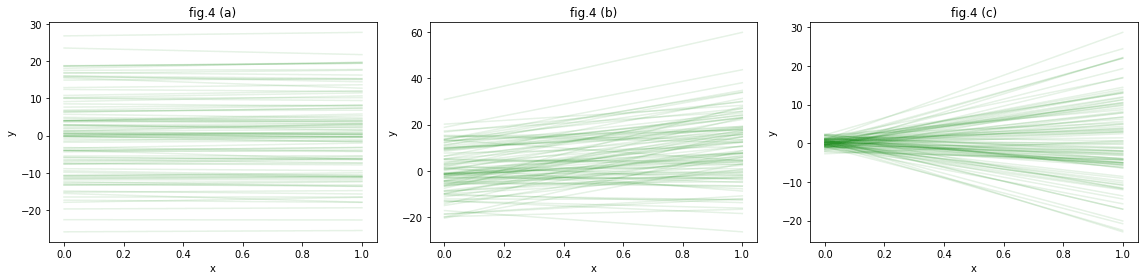
例として、次のfig.4の３つのグラフでは次のような事前分布を設定したものを可視化しています。

(a)：pm_aの標準偏差sdを小さくした場合。（sd=1.0） 傾きの範囲が制限されます。

# (a)の事前分布

  pm_a = pm.Normal('pm_a', mu=0.0, sd=1.0)
  pm_b = pm.Normal('pm_b', mu=0.0, sd=10.0)

(b)：pm_aの平均値muを大きめにした場合。（mu=10.0） 傾きがプラスの値になる傾向が強くなります。

# (b)の事前分布

  pm_a = pm.Normal('pm_a', mu=10.0, sd=10.0)
  pm_b = pm.Normal('pm_b', mu=0.0, sd=10.0)

(c)：pm_bの標準偏差sdを小さくした場合。（sd=1.0） 切片がゼロ付近になる傾向が強くなります。

# (c)の事前分布

  pm_a = pm.Normal('pm_a', mu=0.0, sd=10.0)
  pm_b = pm.Normal('pm_b', mu=0.0, sd=1.0)

MCMCの実行

統計モデリングでは、データを「学習」や「予測」する工程は、推論（inference）と呼ばれ、これはアルゴリズムが自動的に行ってくれます。なお、機械学習や深層学習の分野では、大量のデータから傾向を抽出することを「学習」、学習後に予測を行うことを「推論」と呼ぶことが多いですが、統計モデリングでは学習も予測もどちらもまとめて推論と呼ぶ場合が多いことに注意してください。MCMCが代表的な手法ですが、ほかにも汎用性の高い手法として変分推論法（variational inference method）などがあります。PyMC3では、モデルを設計した後、pm.sample()によってMCMCを実行します。

# MCMCの実行

with model_linear:
   posterior_samples = pm.sample(100)

今回の例ではMCMCは数秒程度で終了しますが、データ量やモデルの複雑さによっては、完了まで多大な計算時間を要することもあります。posterior_samplesには、MCMCによって複数抽出された傾きおよび切片が100個格納されています。それぞれ可視化してみましょう。

# 予測の可視化

X_range = np.linspace(0, 1, 1000)
plt.figure()
for i in range(100):
  plt.plot(X_range, [posterior_samples['pm_a'][i] * x + posterior_samples['pm_b'][i] for x in X_range], 'g-', alpha=0.1)

plt.scatter(X, Y)
plt.xlabel('x')
plt.ylabel('y')

fig.5の実行結果を観察してみましょう。 MCMCによって抽出された複数の直線の集まりを見ると、予測に対する不確実性（uncertainty）が表現されていることがわかります。 つまり、この直線の１つ１つが、実際の４個のデータの背後に存在している法則（今回の場合は直線）の候補を表しています。データが密集している真ん中（x=0.5あたり）では、予測に対する不確実性は小さく、縦軸の予測値は2.5から5.0あたりに広がっています。一方で、右側のx=1.0あたりでは、予測のブレが大きく、予測値が5.0から15.0あたりまで大きく広がっています。これは、x=0.5よりもx=1.0やそれより先の領域の方が予測が難しいことを示しています。このような不確実性は、予測結果に基づく意思決定を行う際に重要です。例えば、回帰モデルを使って株価を予測する場合、予測の振れ幅が大きい場合には売買の判断を見送るなどが考えられます。予測の不確実性は、モデルが持つ予測の自信度を表しているとも言えます。単純に具体的な数値を当てにいくよりも、このように振れ幅も同時に示すことによって、より正確な判断が行いやすくなります。予測の的中率だけでなく、「わからないときはわからないといえる」というのが、統計的予測を実応用する上では重要です。

もっと練習したい方のために

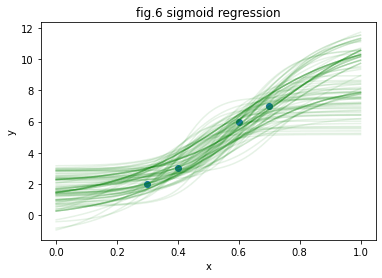
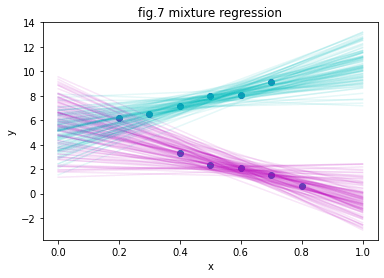
PyMC3を利用したモデリングから予測までの簡単な例を紹介しました。今回紹介した回帰モデルは、工夫次第では様々な拡張を行うことができます。例えば、fig.6は一次関数ではなく、Sの字を描くようなシグモイド関数（sigmoid function）と呼ばれる非線形変換を加えたものです。これは一般化線形モデル（generalized linear model）と呼ばれるモデルの一例になっています。また、シグモイド関数を何層にも重ね合わせるとニューラルネットワーク（ニューラルネットワーク）と呼ばれるモデルが作れます。また、fig.7は２本の異なる回帰関数を組み合わせた予測で、混合モデル（mixture model）の例となっています。解析対象の個体差など、データが従う法則が背後に複数存在すると考えられる場合に有効な手法です。このような例だけではなく、モデルの発展のさせ方はアイデア次第で無数に存在します。シンプルなモデルから使い方を学び、ご自身の取り組んでいる分析課題を解決するために少しずつモデル拡張を行っていくのが、最も効率の良い統計モデリングの学習方法です。

今回紹介した線形回帰やその応用モデルは下記のGoogle Colaboratoryのページに置いてあります。Googleアカウントを持っていれば、Colaboratory上で無料で実行し、動作確認を行うことができます。
https://colab.research.google.com/drive/1SoOK1OpLgQAmglp1ORaovEe9XBIlYR8X

フリサポ フリサポ
BIG DATA NAVI BIG DATA NAVI
プログラミング

関連記事Related Posts