使える統計モデル10選(後編)
前回の記事では、使える統計モデル10選の前編として、主に回帰モデルに焦点を絞って紹介しました。
今回はその後編に当たる生成モデル編です。生成モデル(generative model)は、端的に言うと、コンピュータシミュレーションによりデータを人工的に作ることができるモデルです。データが作られる過程をうまく表現したモデルを構築することができれば、予測だけではなく異常検知やデータ圧縮など幅広いタスクに応用することができます。
目次
生成系(教師なし系)
回帰モデルと同様、生成モデルも数個のパラメータから構成される簡単なものから、複数のモデルを巧みに組み合わせた複雑なものまで無限に存在します。ここでは、データ圧縮から自然言語処理、ソーシャルネット解析までさまざまなデータ解析のタスクで利用されている代表的な生成モデルを5つ選んで紹介します。また、生成モデルのすべては潜在変数モデル(latent variable model)の一例となっています。
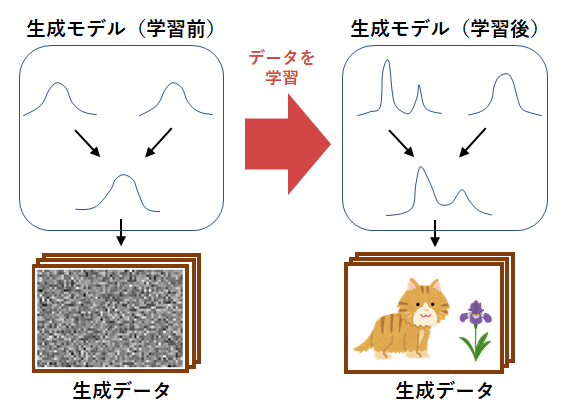
ここでは正確な議論を省いて、生成モデルの仕組みを簡単に解説します。図1は生成モデルの概念図です。生成モデルは、確率分布(probability distribution)と呼ばれるランダムな数値を出力する仕組みを組み合わせることによって構築されます。図の例では、左側の学習前のモデルは確率分布がまだ学習されていないため、乱雑なノイズのみしか生成できていません。大量の画像データをモデルに学習させることによって、背後にある確率分布が適応的に変化し、結果として右側のようにモデルがデータの生成過程を獲得します。
前回紹介した回帰モデルと同様、データに対してどのようなモデルを利用するかは分析者に依存します。同じ学習データに対しても、与える生成モデルが変われば結果の解釈や解決可能な問題の種類が変わっていきます。生成モデルに関しても、あらゆるデータに潜む生成過程を完全に抽出できるような万能なモデルは存在しません。したがって、ここでも解析の目的やデータの特性に応じて、適切な生成モデルを選択または設計する必要があります。
行列分解モデル
行列分解モデル(matrix factorization model)は非常に用途の広い教師なし学習モデルで、データの非可逆圧縮や、特徴的なパターンの抽出などに用いられます。
ここでは音声データに対して行列分解モデルを適用し、パターン抽出を行う事例を見ていきます。図2の中央のグラフは7秒程度のオルガンの演奏を録音した音声データに対して、高速フーリエ変換(fast fourier transformation)による周波数解析を行ったものです。簡単に言うと、横方向の軸が経過時間を表し、縦方向が周波数の強さを示しています。例えば、音声データの最初の方では低周波の成分(0~2,000Hz)が強くなっており、後半ではやや高周波の成分(2,000~15,000Hz)が登場していることがわかります。これは前半で低い音の和音を弾き、後半で高い音の和音を弾いたためです。
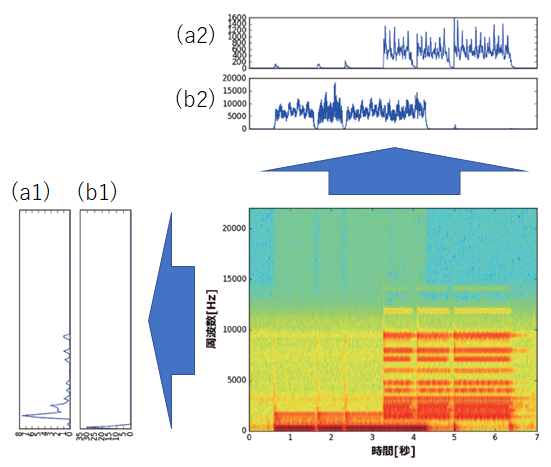
図2には、行列分解手法の1つである非負値行列因子分解(nonnegative matrix factorization)を適用した結果も同時に示しています。元々のオルガンの演奏データが、図中の(a1)、(b1)、(a2)および(b2)に分解されています。(a1)や(b1)は、分解によって得られた「和音」を表現しているといます。(a1)には高周波の和音、(b1)には低周波の和音が抽出されています。(a2)や(b2)は、それぞれの和音が押されたタイミングを表しています。(a2)を見ると高周波の和音が演奏データの後半の方に登場してくることがわかります。同様に、(b2)では低周波の和音が前半に登場していることがわかります。
このように、行列分解は元々のデータに対するよりコンパクトな表現(コード)を抽出することによって、データの圧縮を行ったり、データに潜む典型的なパターンを抽出することに利用できます。類似の手法としては主成分分析(principal component analysis)、因子分析(factor analysis)、k平均法(k-means clustering)、ベクトル量子化(vector quantization)などが存在し、それぞれこのような「コード化」を行うための数学的前提が異なるモデルになっています。
混合モデル
混合モデル(mixture model)は、複数個の異なるデータの生成過程を組み合わせて表現するための手法です。主にデータを分割するクラスタリング(clustering)や回帰予測に用いられます。
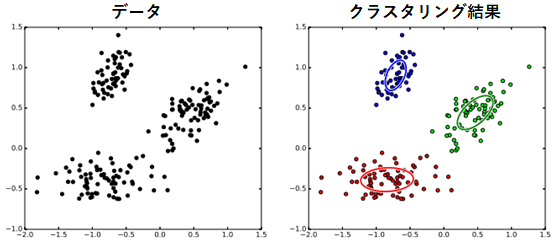
例えば図3の左側のような散布図で表現された2次元のデータがあったとします。クラスタリングの目的は、このデータの集合に対して、ある「まとまり」を自動的に抽出することです。図3の右側では、このデータに対してガウス混合モデル(Gaussian mixture model)を利用してクラスタリングを行ったものです。この図のガウス混合モデルでは、3つの異なる生成過程が仮定されており、それぞれの生成過程はガウス分布(Gaussian mixture model)あるいは正規分布(normal distribution)によって表現されています。
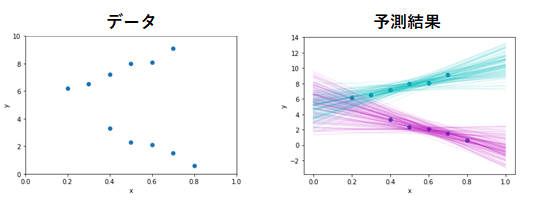
混合モデルのアイデアは回帰モデルにも利用することが可能です。図4は、前回記事で紹介した線形回帰モデルに対して混合モデルのアイデアを組み合わせたものです。複数の直線を仮定することによって、自動的にデータのクラスタリングと、それに応じた適切な予測が得られています。前回解説した階層ベイズモデルによる回帰と似ていますが、こちらの混合回帰モデルは、データの1つ1つがどちらのクラスに所属しているかの情報を与えなくても、データから推測できる点が異なっています。
状態空間モデル
状態空間モデル(state space model)は、主に時系列データの解析に用いられます。
典型的な使用例としては、移動物体の位置推定があります。移動物体の位置はGPSなどを利用して測地することができますが、測定値は常に誤差を含んでいると考えられます。状態空間モデルでは、移動物体の真の位置を、直接観測できない状態(state)と考え、その状態にノイズが付加されて観測データが得られていると仮定します。また、真の状態は、一時刻前の状態に依存して決定されるように仮定されます。これは例えば「移動物体は急峻に別の位置へワープすることはないだろう」という仮説などに基づいて設計されます。
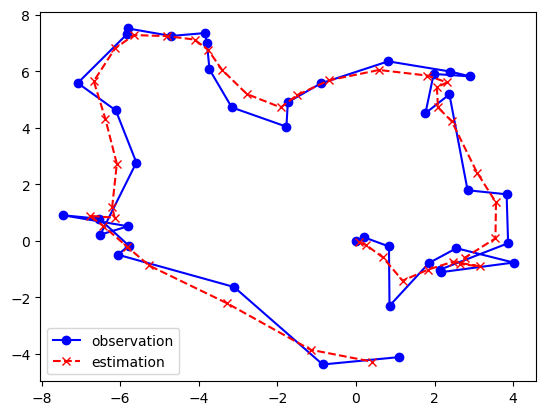
図5は状態空間モデルの一つである線形動的システム(linear dynamical system)と呼ばれるモデルを使って物体の位置推定を行った例です。青●で示されているのが実際に観測された位置データの軌跡です。それに対して、線形動的システムを使って観測ノイズの成分を取り除いた結果が赤×で示されている軌跡です。観測データに存在するブレが軽減され、滑らかな推定結果が得られていることがわかります。なお、このような線形動的システムによる推定は、 カルマンフィルタ(Kalman filter)として知られるアルゴリズムの一般化になっています。
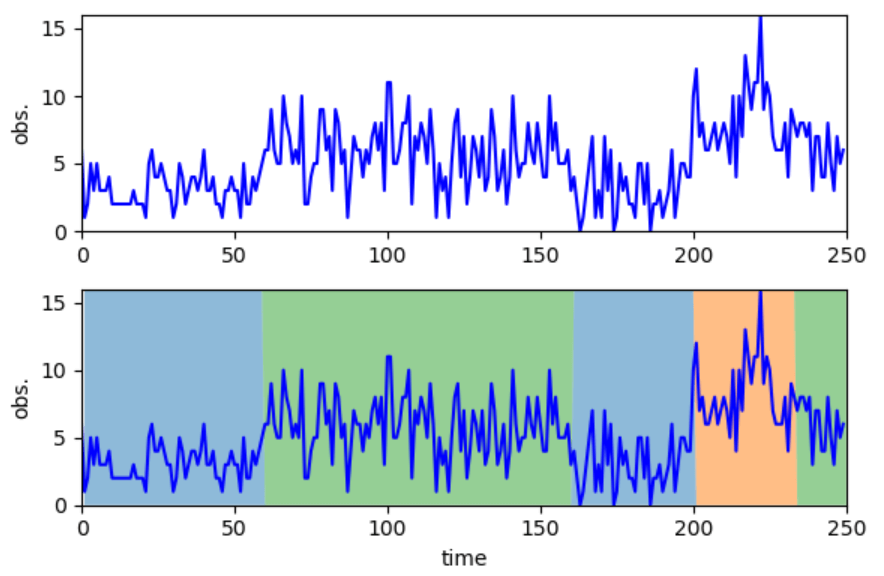
状態空間モデルは、状態が離散の値を取る場合は特に隠れマルコフモデル(hidden Markov model)と呼ばれます。隠れマルコフモデルは、時系列データの将来予測はもちろん、時系列データのクラスタリング(分割)にも用いられます。図6は隠れマルコフモデルを用いて、長さが250の時系列データを分割した例です。観測データの値に応じて、データがそれぞれ3色で表される3種類の領域に分割されていることがわかります。このような時系列解析は、データの変化点検知や異常検知、数値の将来予測などに用いることができます。
トピックモデル
トピックモデル(topic model)は自然言語で書かれた文書を解析するためのモデルで、文書を意味内容を抽出することができます。応用事例としては、ニュース記事の分類・推薦や、類似文書の検索などがあります。最もシンプルなものにLDA(latent Dirichlet allocation)があります。LDAでは、文書に対して潜在的なトピック(政治、スポーツ、音楽など)が背後に存在していると考え、そのトピックに基づいて文書中の単語の出現が決まってくると仮定します。
図7はLDAを使って文書の解析を行った結果です。上に並んでいるArts(芸術)やBudgets(予算)は、大量の文書データをLDAによって解析することによって自動抽出されたトピックです。例えば、ArtsにはNEW(新しい)やFILM(映画)、MUSIC(音楽)などの単語が良く使われる傾向にあることを示しています。その下にあるのは、実際に解析した文書の一部です。1行目を見ると、Foundation(財団)という単語が緑色のBudgetsに分類されていることがわかります。
![図7 LDAによる文書解析[Blei DM, Ng AY, Jordan MI, 2003]](https://www.bigdata-navi.com/aidrops/wp-content/uploads/2020/04/image-6-1.png)
トピックモデルは様々な拡張が提案されてきており、自然言語処理に携わっていないデータサイエンティストでもアイデア収集のために極めて有用です。標準的なLDAは、単語の前後のつながりを考慮していない単純なモデルになっていますが、時系列モデルのアイデアを組み合わせることにより、単語間の依存関係を考慮したモデルへ拡張することも可能です。また、文書に対するメタ情報(筆者や執筆年など)を盛り込んで解析するようなモデルもあります。
確率的ブロックモデル
確率的ブロックモデル(stochastic block model)は、ネットワークを解析するために用いられるモデルです。例えば、SNSにおける友達関係のつながりなどが解析対象になります。確率的ブロックモデルを用いれば、つながりのネットワークの中からコミュニティ(クラスター)を発見したり、つながりを予測することによって友達候補を推薦することなどができます。
ネットワークは、ノード(点)とエッジ(線)から成り立ちます。ソーシャルネットワークの例では、ノードはユーザー、エッジは友達関係を示します。図8ではそのようなネットワークデータから、自動的に3つのクラスターを抽出した結果になっています。

確率的ブロックモデルは他の統計モデルと同様、モデルに工夫を加えることによってさまざまなデータを多角的な観点で分析することができます。図8は「各ユーザーがそれぞれ単一のグループに所属する」という観点で分析を行った結果ですが、通常は各ユーザーに対して「会社の同僚」「親戚」「同級生」「地域住民」など、複数の所属先が同時に存在すると考えるのが妥当でしょう。このようなマルチグループを仮定した解析も確率的ブロックモデルの興味の対象になります。また、Eメールの取引データなどを解析する際には、メールが送信されたタイミングなどの時間情報がデータとして残っている場合が多く、時系列モデルと確率的ブロックモデルを組み合わせて解析するような方法もあります。
生成モデルと計算コスト
統計モデルを利用するにあたり、データの学習や予測に関わる計算時間や必要メモリを考えるのは極めて重要です。これは特にパーソナライズされたサービスを開発する際などには顕著になります。例えば、1クリック10円の報酬額がかかる広告配信に対して、1回で20円かかるようなリッチな広告推薦アルゴリズムを採用するのはあまり意味がないでしょう。また、一般的に、統計モデルに関わる計算コストとと、解析によって得られる結果の精度との間にはトレードオフの関係があります。例えば、予測精度が高いとされるアルゴリズムAよりも、計算時間が100分の1で済むアルゴリズムBを100倍の時間をかけてチューニングする場合の方が結果が良くなる場合もあります。
一般的に、生成モデルは回帰モデルより計算コストがかかるケースが多く、利用を検討しているモデルの計算時間・必要メモリを確認する必要があります。生成モデルの計算コストが高くなる理由は、主に潜在変数(latent variable)の存在にあると言えます。統計モデル上では、潜在変数はデータの発生源であり、いわば“種”のようなものです。例えば、100枚の画像を生成モデルによって生成するためには、100個の潜在変数が“種”として必要になります。逆に、学習データに対してある生成モデルを適用して学習や解析を行うということは、この100個の“種”を計算によって明らかにする必要があります。このように潜在変数モデルはデータ数に比例して推定すべき値が増えていきます。逆に言えば、データ数がそれほど多くない場合などは、潜在変数の計算コストはあまりかかりません。
近年では潜在変数の推定を効率的に計算するアルゴリズムが開発されてきており、多くのモデルに汎用的に使える手法から、特定のモデルの計算に特化したものまで幅広く存在します。適用するモデルだけでなく、そのモデルを使った計算がどのようなアルゴリズムを利用しているかまで気を配れるようになると良いでしょう。
モデルをどのように評価するか
生成モデルに限らず、一般的に機械学習や統計のモデルを応用する際は、解釈性、予測性能、拡張性、保守性、さらに前述の計算コストなどによって評価を行う必要があります。各要素の重要性は、取り組んでいる課題によって異なります。近年では予測性能に偏りがちですが、感覚的には、これらの要素はどれも平等にケアする必要があります。
解釈性は統計モデルにとって最も重要な評価視点です。これは、単純に「統計モデルから得られた結果が何を意味するか」といったことに関してあれこれ議論するものではありません。より重要な視点は、「統計モデルから得られた結果をもとにして、どのような行動が実行できるのか」ということが明確かどうかである点です。例えば、明日の天気を予測する2つのアルゴリズムA、Bがあったとします。アルゴリズムAは高い精度で「晴天」または「雨天」のいずれかの予測結果を示します。一方でアルゴリズムBは、降水確率を出力します。この場合、明らかにアルゴリズムBの方が、提供してくれる情報量としては大きく、解釈性も良いと言えます。例えば、「傘を持っていくかどうか」「洗濯物を干すべきかどうか」などの選択は個人の判断によっても変わってくるため、単純に「晴天」か「雨天」かを示されるよりも、確率を示してくれる方が判断に有用な場合が多いでしょう。「行動に必要な情報が提供されるか」が解釈性において重要な視点です。なお、この「行動」を行う主体に関しては必ずしも人間である必要性はありません。ある統計モデルから出力された情報をもとに、別のシステムが自動的に処理を実行する場合もこれに含まれます。統計モデルに求められる解釈性とは、「人間が理解できること」とはイコールではないことに注意が必要です。
予測性能は、単純に統計モデルによって予測された値がどれだけ真の値に近かったかを評価する方法です。回帰モデルなどでは、学習データとテストデータを分け、テストデータによって予測の答え合わせをして性能を評価するケースがほとんどです。生成モデルの場合は目的によって評価手段が変わっていきます。例えば、データ中の欠測値を予測したい場合は、回帰モデルと同様にテストデータの答え合わせの方法を使って評価することができます。
拡張性も非常に重要です。一般的に、統計モデルは作ってそれでおしまいということはあまりなく、その後もモデルの改善は継続されていきます。例えば、トピックモデルや確率的ブロックモデルの節でも解説したように、ある統計モデルを構築した際には、それに加えてさらに別のアイデアを追加したり、別のモデルを組み合わせるなどして、データからより深い洞察を得られるようになります。「データの時間的な変動を考慮したい」「異なるフォーマットのデータも利用できるようにしたい」「動画像データだけではなく音声データも組み合わせて解析したい」などは、すべてモデル拡張の方向性です。利用しているモデルが、将来発生しそうな需要に対応できるかどうかも重視するべきです。
機械学習を利用したサービスなどを運用する際には、保守性は極めて重要な要素になっていきます。拡張性に関する議論でも説明したように、モデルの改善は継続的に必要です。なぜならば、データは時間を経るごとに絶えず変化するからであり、それに合わせてモデルを適宜修正する必要があるからです。重要な点は、チームが明確な指針を持ってモデルやアルゴリズムを設計することにあります。その場しのぎの対処療法的な修正を何重にも重ねていくと、ソースコードが複雑化し、いったいどのアイデアがどのような効果を生むのかがわかりにくくなっていきます。このような改善はいつか破綻します。チームが課題意識を共有し、個々の課題と解決手段を明確に捉えることによって、破綻の道はある程度防ぐことが可能です。
まとめ
今回は比較的使用頻度の高い統計モデルを、私の独断と偏見で10個紹介させていただきました。
これらのモデルは必ずしも独立したものではなく、互いに深い関係性があります。例えば、一般化線形モデルを再帰的な構造に拡張したものがニューラルネットワークだと言えます。また、各モデルは原理的には自由に組み合わせることが可能です。例えば、一般化線形お出るに状態空間モデルを繰り返せば、正規分布に従わない複雑な傾向を持つデータの時系列予測が可能になります。様々なモデルの関連性や組み合わせ方を学ぶことによって、統計モデリングに関してより深い理解と柔軟な応用力を身に着けることができるようになります。
これらの統計モデルの設計や利用を行う際には、確率的プログラミング言語(probabilistic programming language)を利用するのが便利です。これに関しては、次の入門記事があります。
Pythonで作って学ぶ統計モデリング
参考文献
須山敦志,杉山将.ベイズ推論による機械学習入門.講談社(2017)
須山敦志.ベイズ深層学習.講談社(2019)
Blei DM, Ng AY, Jordan MI. Latent dirichlet allocation. Journal of machine Learning research. 2003;3(Jan):993-1022.

国内メーカーの研究職,UK のスタートアップの研究職を経て,現在はデータ解析に関するコンサルティングに従事.ブログ「作って遊ぶ機械学習。」にて実践的な機械学習技術に関する情報を発信中.
twitter ID:@sammy_suyama
ブログ:http://machine-learning.hatenablog.com/
著書:ベイズ推論による機械学習入門 講談社(2017),ベイズ深層学習 講談社(2019)

 フリーランス求人を探す
フリーランス求人を探す






